** 본 게시글은 아래 링크를 참고하여 학습을 위해 재정리한 것이며, 모든 저작권은 아래 사이트에 있습니다.
| Ⅵ. 통계적 추론(신뢰구간과 표본크기) 신뢰 구간의 의미 신뢰구간 (Confidence Interval) 신뢰도와 신뢰구간의 의미 |
신뢰구간과 관련된 개념은 봐도 봐도 헷갈리는 것 같다. 이번 포스팅을 계기로 확실하게 공부하고 넘어가자!!!!
신뢰구간과 신뢰도의 개념에 대해 살펴보기 전에 먼저 '추정'과 '추정 가치'에 대해 알아보자.
추정 가치의 개념
- 표본의 정보를 활용해 모집단의 특징을 추측하는 것

- 모집단의 평균인 모평균 μ를 추정한다고 할 때, 모평균이 속할 범위를 1 <= μ <= 10000라고 추정한다면, 100% 확실한 추정임
- 하지만, 추정 범위가 너무 넓어 모평균으로 추정될 수 있는 값이 많기 때문에 추정 가치가 없다고 볼 수 있음

- 반대로, 모평균이 속할 범위를 98 <= μ <= 102라고 추정한다면, 추정범위가 적어 오차가 생길 가능성이 높아짐
- 또한, 추정될 수 있는 값이 몇 개 없기 때문에 추정 가치가 높다고 볼 수 있음
통계적 추론이란?
- 일상생활과 학문적 연구에서, 모집단의 성격을 모르는 상황에서 모집단의 성격을 규명해야 할 때가 많이 있음
- 이때, 모평균이나 모분산과 같은 모수에 대한 어떤 결정을 내리기 위해 모집단에서 표본을 추출해 이를 기반으로 추론함
- 통계적 추론은 모집단의 일부인 표본으로부터 전체 모집단의 성질을 추론해내는 것이기 때문에, 100% 확신할 수 없음
✅ 따라서, 통계적 추론을 할 때는 그 결론의 부정확한 정도를 반드시 언급해야 함
신뢰구간과 신뢰수준((신뢰도)의 개념
- 신뢰구간은 일상생활에서도 많이 쓰이고 있는 개념임
- 예를 들어, 버스를 타고 집에 가는 길에 '언제쯤 도착이야?'라는 카톡에 대한 답변으로 '10~15분 정도 걸릴 것 같아'라고 답변했다면, 10에서 15 사이라는 신뢰구간을 사용한 것임
- 10에서 15 사이라는 값은, 지금까지 내가 여러 번 이 버스를 타봤을 때(표본 추출) 걸리는 시간의 평균값(표본 평균)으로부터 얻어진 것임
- 신뢰구간은
- 모수가 실제로 포함될 것으로 예측되는 범위임
- 추정량의 분포를 이용해 표본으로부터 모수값을 포함하리라고 예상되는 구간을 제시한 것
- 집단 전체를 연구하는 것은 불가능하므로, 샘플링 된 데이터를 기반으로 모수의 범위를 추정하기 위해 사용됨
✅ 따라서, 신뢰구간은 샘플링 된 표본이 모집단을 얼마나 잘 대표하는지 측정하는 방법 - 신뢰수준(신뢰도)은 모수를 포함할 확률을 말하며, 보편적으로 95%와 99%를 사용함
- 신뢰수준이 커지면 구간추정의 폭이 넓어지고, 신뢰수준이 작을수록 구간추청의 폭이 좁아짐
- 신뢰구간이 좁을수록 모집단 추정치가 정확해지며, 일반적으로 표본 크기가 클수록 신뢰구간이 좁아짐
✅ 따라서, 표본이 클수록 더 정확하게 모집단에 대해 더 정확하게 추정할 수 있음

신뢰도에 따라 신뢰구간 구하는 방법
- 크기가 n인 표본평균이 x̄일 때, 모평균 μ에 대한 신뢰도 95%의 신뢰구간

- 크기가 n인 표본평균이 x̄일 때, 모평균 μ에 대한 신뢰도 99%의 신뢰구간(0.95가 아니라0.99로 정정)

- 정리하자면,
정규분포 N(μ, σ²)인 모집단에서, 크기가 n인 표본을 임의로 추출한 표본평균이 x̄일 때,

- 그러나, 변량이 매우 많기 때문에 모집단의 평균과 분산을 알기 어려움
✅ 표본표준편차를 s라고 하고, σ(모표준편차) 대신 s를사용한다면, 모집단의 변량보다 작기 때문에 상대적으로 구하기 쉬움

신뢰도, 표본의 개수, 표본표준편차에 따른 신뢰구간의 변화
- 이를 이해하기 위해서는, 본 글의 맨 처음에 짚고 넘어갔던 추정의 가치에 대한 이해가 필요함!
- 두 구간 모두 n이 같을 때, 신뢰도 95%와 99%의 신뢰구간 비교

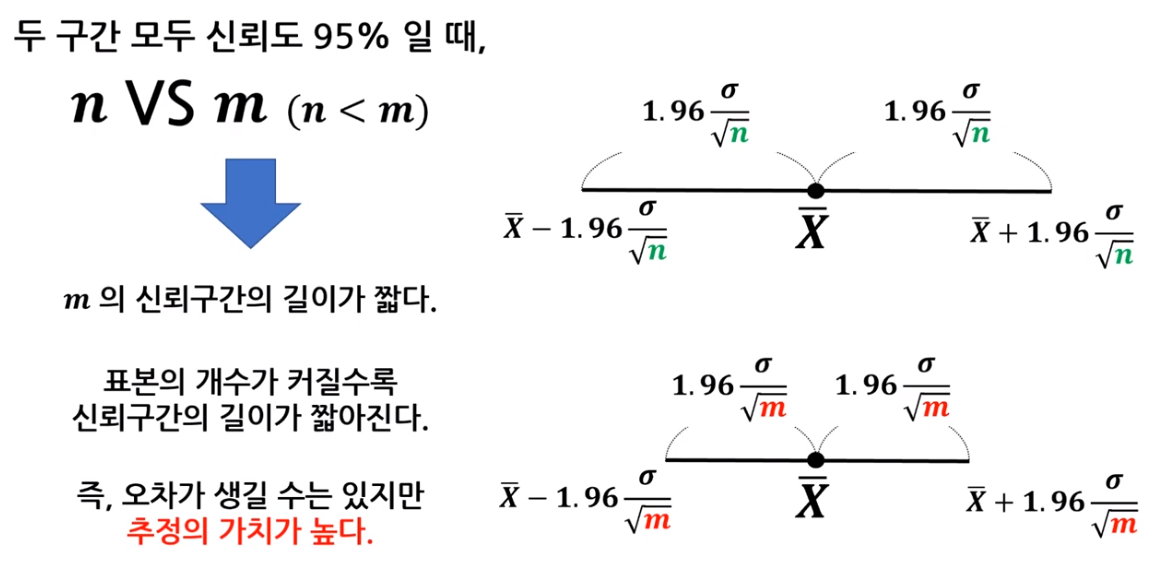
- 두 구간 모두 신뢰도 95%일 때, n과 m 비교(n<m)
정리
- 크기가 n인 표본을 임의로 추출한 신뢰도 95%의 신뢰구간의 의미

- 이 표본들로 모평균을 추청하는 것임

- 각 표본마다 신뢰구간의 위치와 길이가 모두 다름


- 결론적으로, 신뢰도 95%인 모평균μ의 신뢰구간이 의미하는 바는, 표본의 크기가 n인 표본을 계속 추출해서 신뢰구간을 구하는 일을 반복한다면, 그 신뢰구간의 95% 정도가 모평균 μ를 포함한다는 것임
'Study > 통계' 카테고리의 다른 글
| [통계 개념 정리 4] 1종 오류와 2종 오류 (1) | 2023.08.28 |
|---|---|
| [통계 개념 정리 2] p-value(유의 확률) (0) | 2023.08.23 |
| [통계 개념 정리 1] 귀무가설과 대립가설 (0) | 2023.08.22 |