LSTM 기본 개념 및 구조

LSTM이란?

순환 신경망(RNN)의 구조에 장/단기 기억을 가능하게 설계한 신경망의 구조

• RNN의 Gradient Vanishing/Exploding Gradient를 해결하기 위해 고안
• 기억셀을 추가하여 경사 소멸 문제를 해결

LSTM이 RNN의 한계를 극복하기 위한 모델이라고 하니까 일단 RNN부터 살펴보자.

 

 

 

RNN(Recurrent Neural Network)이란?

입력과 출력을 시퀀스 단위로 처리하는 시퀀스(Sequence) 모델

• 시간적으로 상관관계가 있는 데이터에서 주로 사용됨
• Sequence : 말 그대로 순서가 있는 data
• Sequence Model : Sequence data를 다루는 모델. 대표적으로 RNN, GRU, LSTM등

 

 

• 현재 시점의 입력값에 대한 가중치의 곱과 전 시점의 hidden state와 그 가중치 곱의 합을 구한 후 활성화함수 tanh를 적용
• 시간을 많이 거슬러 올라갈수록(long term) 경사를 소실하는 문제가 있음 → Gradient Vanishing 문제
• RNN은 출력과 먼 위치에 있는 정보를 기억할 수 없음(Long-Term Dependencies Problem)
• 시퀀스가 있는 문장에서 문장 간의 간격(gap, 입력 위치의 차이)이 커질 수록, RNN은 두 두 정보의 맥락을 파악하기 어려워짐
• 따라서, 한참 전의 데이터도 함께 고려하여 출력을 만들어보는 것이 LSTM의 목적

 

 

 참고) Gradient Vanishing(기울기 소멸 문제)이란?

역전파 과정에서 입력층으로 갈 수록 기울기(Gradient)가 점차적으로 작아지는 현상 -> hiden layer가 깊어질수록 심해짐

• Back Proagation 과정 중에 시그모이드를 미분한 값을 계속 곱해주면서 Gradient 값이 앞 단의 layer로 올수록 0에 수렴하는 현상이 발생함
• 기울기가 거의 0으로 소멸되어 버리면 네트워크의 학습은 매우 느려지고, 학습이 다 이루어지지 않은 상태에서 멈춤
• 시그모이드 함수와 같은 경우 출력 값이 1 아래여서 기울기 소멸 문제가 빠르게 일어남(0보다 작은 수 끼리 계속 곱하면서 연산했을 때 값이 0에 가까워짐)

 

 

참고) Gradient Exploding이란?

 

• 기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 결국 발산되는 현상
• 다음 챕터에서 배울 순환 신경망(Recurrent Neural Network, RNN)에서 쉽게 발생할 수 있음

 

 

 

LSTM의 구조

 

• LSTM은 hidden state만이 아니라 cell state가 있으며 Forget gate, Input gate, Output gate를 통해 계산이 이루어짐
• 어떤 정보를 잊을지 유지할지를 선택하여 long term과 short term에 대한 정보를 고려할 수 있음
• gate는 forget, input, output 총 3개가 있음
• 세 개의 gate 모두 활성화함수로 시그모이드를 적용하고 σ로 표현함
• 위에서 말했듯이 gate는 cell state와 함께 정보를 선택적으로 활용할 수 있도록 함

LSTM의 기본 구조

 

 

STEP 1. Forget Gate: 과거 정보를 잊을지 말지 결정하는 과정

 

 

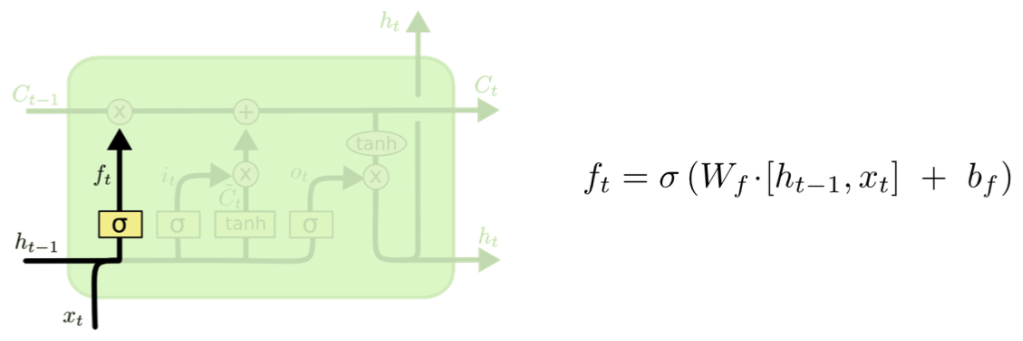
• forget gate는 과거 정보를 기억할지 잊을지를 결정하는 단계
• 현재 시점 t의 x값과 이전 시점 t-1의 은닉 상태가 시그모이드 함수를 지나게 됨
• 시그모이드 함수를 지나면 0과 1 사이의 값이 나오게 되는데, 이 값이 곧 삭제 과정을 거친 정보의 양임
  • ex) 0.2가 나오면 “20%만큼 기억해라”
• 0에 가까울수록 정보가 많이 삭제된 것이고 1에 가까울수록 정보를 온전히 기억한 것
• forget gate의 연산으로 나온 f(t)는 ‘과거 정보에 대해서 얼마나 잊었냐/기억하냐를 가지고 있는 값'임

 

 

 

Step 2. Input Gate: 현재 정보를 저장할지 결정하는 과정

 

 

• 현재 정보를 잊기/기억하기'를 위한 gate
• 현재 시점 t의 x값과 입력 게이트로 이어지는 가중치 W(xi)를 곱한 값과, 이전 시점 t-1의 은닉 상태가 입력 게이트로 이어지는 가중치 W(hi)를 곱한 값을 더하여 시그모이드 함수를 지나는데 이를 i(t)라고 함
• 그리고 현재 시점 t의 x값과 입력 게이트로 이어지는 가중치 W(xi)를 곱한 값과 이전 시점 t-1의 은닉 상태가 입력 게이트로 이어지는 가중치 W(hg)를 곱한 값을 더하여 하이퍼볼릭탄젠트 함수를 지나는데 이를 g(t)라고 함
• 시그모이드 값은 0~1 사이의 값을, tanh는 -1~1 사이의 값을 갖기 때문에 0< i <1, -1 < g < 1을 만족함
• i(t)는 forget gate와 마찬가지로 0에 가까울수록 많은 정보를 삭제하는 것을 의미
• 반면 g(t)는 -1~1 사이의 값을 갖는데 나중에 현재 정보를 cell state에 얼마나 더할지를 결정하는 역할

 

 

 

Step 3. Cell State Update: 과거 cell state(Ct-1)를 새로운 state(Ct)로 업데이트 하는 과정(장기 상태)

 

 

• 입력 게이트에서 구한 i(t), g(t)에 대해서 원소별 곱(entrywise product)을 진행
  • 원소별 곱 : 같은 크기의 두 행렬이 있을 때 같은 위치의 성분끼리 곱하는 것
• f(t)○C(t-1)의 계산을 통해 이전 시점의 cell 정보를 얼마나 유지할지를 구함
• i(t)○g(t)를 통해 현재 기억할 정보를 구함
• '과거에서 유지할 정보' + '현재에서 유지할 정보'를 통해 현재 시점의 cell state를 업데이트 함
• 이 값은 다음 t+1 시점의 LSTM 셀로 넘겨짐

 

일반적인 RNN은 곱하기로만 이루어져 있는데, LSTM은 더하기로 잇고 있음. 따라서, Gradient Vanishing 문제가 없는 것임. 이는 ReLU를 사용하지 않고, tanh를 사용하고도 순환신경망에서 Gradient Vanishing 문제를 해결할 수 있는 핵심적인 부분

 

 

 

Step 4. Output Gate (hidden state): 어떤 출력값을 출력할지 결정하는 과정

 

 

• Cell 상태에 기반을 두지만 Filtered된 버전
• Sigmoid층을 동작해서 어떤 부분을 출력할지 결정
• 그 후 -1~1 사이값을 갖도록 cell을 tanh에 넣음
• tanh와 sigmoid출력 게이트와 곱함